تاریخ : شنبه 87/3/4 | 12:38 عصر | نویسنده : روح الامین
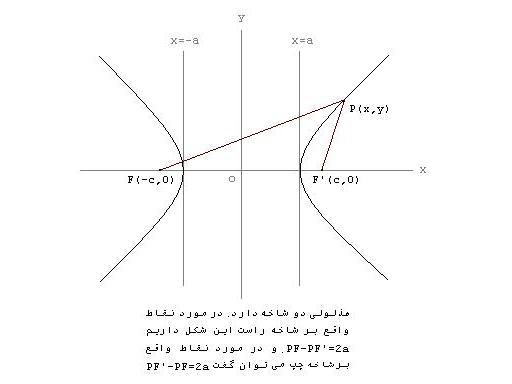
هذلولی
تعریف
هذلولی مجموعه نقاطی از صفحه است که تفاضل فواصل هر یک از آن ها از دو نقطه ی ثابت در صفحه مقدار ثابتی باشد.کاربرد
مسیر های هذلولوی در نظریه نسبیت اینشتین مطرح می شوند و اساس سیستم هوانوردی رادیویی لوران LORAN: Long Range Navigation - - نیز هستند. مسیر ستاره ی دنباله داری که به خورشید خودش بر نمی گردد، هذلولوی است ( احتمال اینکه سهموی باشد صفر است ).تلسکوپ های بازتابنده نظیر تلسکوپ 200 اینچی هاله 2 ، واقع در کوه
پالومار کالیفرنیا، و تلسکوپ فضایی ناسا که قرار بوده در 1988 به فضا
پرتاب شود، از آینه های هذلولوی کوچک، همراه با آینه های سهموی بزرگتر
استفاده می کنند.

معادله ی هذلولی
با در نظر گرفتن دو نقطه ی ثابت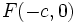 و
و  موسوم به کانون ها و مقدار ثابت
موسوم به کانون ها و مقدار ثابت 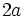 ، آن گاه نقطه ای چون
، آن گاه نقطه ای چون  بر هذلولی واقع است اگر و تنها اگر:
بر هذلولی واقع است اگر و تنها اگر:
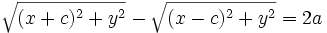
یا

معادله ی دوم نظیر معادله ی اول می باشد، با این تفاوت که به جای
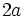 ،
، 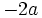 قرار گرفته است. لذا می توان در اولی نوشت
قرار گرفته است. لذا می توان در اولی نوشت  ، پس:
، پس:



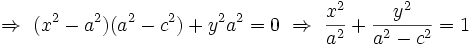
در این جا
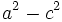 منفی است زیرا تفاضل دو ضلع مثلث
منفی است زیرا تفاضل دو ضلع مثلث 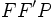 از ضلع سوم کوچکتر است یعنی
از ضلع سوم کوچکتر است یعنی  . لذا
. لذا 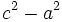 مثبت است و یک ریشه ی دوم حقیقی مثبت دارد که آن را با
مثبت است و یک ریشه ی دوم حقیقی مثبت دارد که آن را با 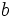 نمایش می دهند، پس:
نمایش می دهند، پس: 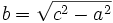
بنابر این معادله ی هذلولی به صورت زیر خواهد بود:
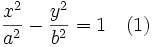
که شبیه معادله ی بیضی است. اختلاف آن ها تنها در علامت منفی موجود در معادله ی هذلولی و رابطه ی جدید بین
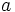 ،
، 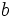 و
و 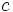 است.
است.
نکته 1: هذلولی نسبت به هر دو محور و نسبت به مبدا متقارن است و با محور
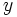 تقاطعی ندارد. در واقع هیچ بخشی از خم بین خطوط
تقاطعی ندارد. در واقع هیچ بخشی از خم بین خطوط 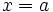 و
و 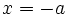 قرار نمی گیرد.
قرار نمی گیرد.
نکته 2: فاصله های
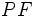 و
و 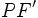 از روابط زیر به دست می آیند:
از روابط زیر به دست می آیند:
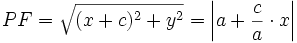
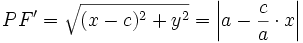
در این جا
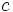 از
از 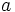 بزرگتر است و
بزرگتر است و 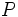 یا در سمت راست خط
یا در سمت راست خط 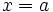 قرار می گیرد (یعنی
قرار می گیرد (یعنی )، یا در سمت چپ خط
)، یا در سمت چپ خط 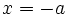 ( یعنی
( یعنی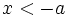 ).
).
نکته 3 : وقتی
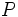 در سمت راست خط
در سمت راست خط 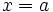 قرار داشته باشد رابطه ی
قرار داشته باشد رابطه ی 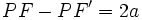 و اگر در سمت چپ
و اگر در سمت چپ 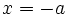 واقع باشد رابطه ی
واقع باشد رابطه ی 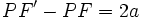 برقرار است.
برقرار است.
مجانب ها
تعریف: اگر هم زمان با دور شدن نقطه ای چون ( واقع بر یک خم ) از مبدا مختصات، فاصله ی آن با خط ثابتی به سمت صفر میل کند، آن گاه چنین خطی را مجانب خم نامند.
( واقع بر یک خم ) از مبدا مختصات، فاصله ی آن با خط ثابتی به سمت صفر میل کند، آن گاه چنین خطی را مجانب خم نامند.
هذلولی
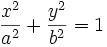 دو مجانب دارد که عبارت اند از خط های
دو مجانب دارد که عبارت اند از خط های 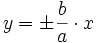 .
.
چرا که عبارت سمت چپ معادله ی هذلولی را می توان تجزیه کرد و معادله را به صورت:
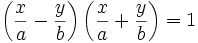
یا

نوشت.
الف) تحلیل معادله ی
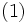 نشان می دهد که یکی از شاخه های خم در ربع اول قرار داشته و تا بی نهایت امتداد دارد. اگر نقطه ی
نشان می دهد که یکی از شاخه های خم در ربع اول قرار داشته و تا بی نهایت امتداد دارد. اگر نقطه ی 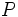 واقع بر این شاخه رفته رفته از مبدا دور شود،
واقع بر این شاخه رفته رفته از مبدا دور شود،  و
و 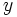 بی نهایت می شوند و عبارت سمت راست معادله ی
بی نهایت می شوند و عبارت سمت راست معادله ی 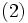 به صفر نزدیک می شود. پس طرف چپ هم باید همین وضع را پیدا کند. در نتیجه:
به صفر نزدیک می شود. پس طرف چپ هم باید همین وضع را پیدا کند. در نتیجه:

ب) وقتی
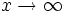 ، مشاهده می شود که:
، مشاهده می شود که:
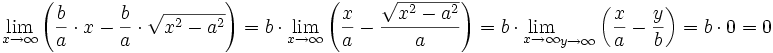
چون فاصله ی قائم بین خط و هذلولی وقتی
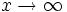 ، به صفر میل می کند، فاصله ی عمودی بین نقاط هذلولی و خط
، به صفر میل می کند، فاصله ی عمودی بین نقاط هذلولی و خط 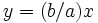 نیز به صفر میل می کند. بنابراین از بندهای (الف) و (ب) نتیجه می شود که خط
نیز به صفر میل می کند. بنابراین از بندهای (الف) و (ب) نتیجه می شود که خط 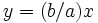 مجانب هذلولی است.
مجانب هذلولی است.
بنابر تقارن، خط
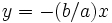 نیز مجانب این هذلولی است.
نیز مجانب این هذلولی است.
نکته: گاه مجانب را چنان تعریف می کنند که لازم است وقتی
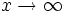 ، شیب خم به شیب مجانب نزدیک می شود. این تعریف نیز در این جا صادق است چرا که:
، شیب خم به شیب مجانب نزدیک می شود. این تعریف نیز در این جا صادق است چرا که:
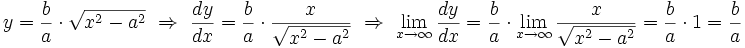
و این همان شیب مجانب
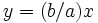 است.
است.

معادلات متعارف هذلولی هایی که محورهایشان با محورهای مختصات موازی اند و مرکزشان در (h,k) واقع است:
الف) اگر خط گذرنده از کانون ها موازی با محور باشد:
باشد:
معادله ی هذلولی:

راس ها:
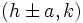
کانون ها:
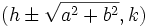
مجانب ها:

ب) اگر خط گذرنده از کانون ها موازی با محور
 باشد:
باشد:
معادله ی هذلولی:
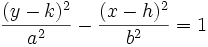
راس ها:

کانون ها:
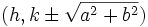
مجانب ها:
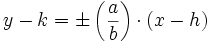
ج) معادلات دو بند فوق را می توان با انتقال
 و
و 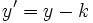 و توجه به این مطلب که معادلات حاصل بر حسب مختصات پریم دار به صورت زیراند به دست آورد:
و توجه به این مطلب که معادلات حاصل بر حسب مختصات پریم دار به صورت زیراند به دست آورد:
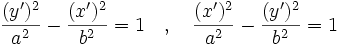
توجه کنید که در معادله ی مجانب مربوط به بند (I)،
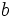 بر
بر 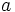 و در معادله ی مجانب مربوط به بند (II)
و در معادله ی مجانب مربوط به بند (II) 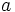 بر
بر 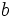 تقسیم می شود.
تقسیم می شود.
.: Weblog Themes By Pichak :.
